Lorsque Valentin passa le portail du collège ce mardi à huit heures moins dix, Charles-Henri Dubois de la Capelle était déjà dans la cour, surveillant de loin les arrivées. Il se dirigea vers son ennemi, visage fermé et lui intima : « Mets-toi à côté de moi en cours de maths. »
— Bonjour à toi aussi, répondit Valentin avec un petit sourire ironique.
Imaginant très bien le pourquoi de cette requête et de cette mine revêche, dès la rentrée en classe, Valentin s'installa dans la seconde rangée à droite de celle de Charles-Henri, place habituellement occupée par Tony Thénard au grand étonnement de ce dernier ainsi que de celui de Gilles et de ses amis. Devant Valentin se trouvait Océane et à sa droite Morgane Joly. Avant que le professeur de mathématiques, monsieur Eric Derrien fasse l'appel, profitant du brouhaha de l'installation des autres élèves, Charles-Henri sortit de son luxueux sac d'école une poche en plastique aux couleurs de la FNAC et la balança sur la table de Valentin.
— Mon père m'a obligé à t'acheter ça, fit-il, tout mon argent du mois ! Je suppose que tu es content de toi !
Sans merci, sans regarder à l'intérieur, sans palper ni soupeser, à l'étonnement du donneur, Valentin fourra le « cadeau » dans son propre sac duquel il sortit trousse et classeur de math.
Monsieur Derrien, surnommé « air de rien » depuis plusieurs générations d'élèves acheva son appel « ...et enfin Valentin Valmont. Ses yeux se portèrent à la place habituelle de celui-ci. Valentin n'est pas là ? »
— Si, ici monsieur, répondit-il en levant le bras.
— Bon, là, pourquoi pas, commenta le professeur. Aujourd'hui nous abordons le théorème de Pythagore. Deux questions, qu'est-ce qu'un théorème ? Qui est Pythagore ? Qui veut répondre ?
Tony et Mathilde levèrent la main immédiatement.
— Tony ?
— Ça ne fait pas deux mais trois questions m’sieur.
— Voilà une remarque bien constructive, Tony, Merci d’avoir participé. Mathilde ?
— Pythagore était un philosophe et mathématicien grec qui vivait il y a plus de deux mille ans.
— Bon Mathilde, disons plus précisément deux mille six cents ans. Il y avait des bons en math à cette époque. Et un théorème ? Oui Gilles.
— Un théorème est une vérité mathématique.
— Ce n'est pas faux mais incomplet. Un théorème est une affirmation mathématique ou logique qui peut être démontrée , c’est à dire un énoncé qui peut être prouvé par un raisonnement logique. Donc ce monsieur Pythagore a énoncé l'affirmation suivante : écoutez bien et regardez le tableau. Dans un triangle rectangle a,b,c, le carré de la longueur de l’hypoténuse que voici, est égal à la somme des carrés des longueurs des deux autres côtés, celui-ci et celui-là. On écrit a²=b²+c². Ceci est l'affirmation. Comment le démontrer, comment le prouver ? C'est ce que nous allons voir en faisant un puzzle : Je reprends notre triangle rectangle et je dessine les carrés appuyés sur les trois côtés comme ça :

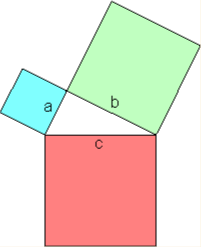
Je vous laisse faire le même dessin sur une feuille de papier Canson, avec soin Clément, la suite en dépend. Peu importe la longueur des côtés du triangle pourvu qu'il soit rectangle. Utilisez la règle et le compas.
Studieuse la classe s'appliqua pendant que le professeur passait dans les travées.
— Bien maintenant il faut prouver que la surface du petit carré bleu plus celle du carré vert égale la surface du grand carré rouge. Pour ce faire, vous allez découper la figure en suivant les contours avec précision, allez-y. Tu n'a pas de ciseaux Marion ?
— J'en ai deux paires, tiens Marion, dit Amandine en lui tendant une paire de ciseaux à ongles.
Maintenant, continua le professeur, vous allez plier votre carton en suivant l’hypoténuse, oui, la ligne c, en laissant les parties colorées à l'extérieur.

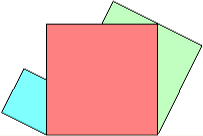
Arrête de souffler Benjamin, ce n'est pas compliqué.
Maintenant découpez la partie bleue et les morceaux verts qui débordent puis dépliez la figure, voici ce que vous obtenez en dépliant la figure :

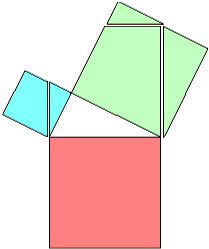
Découpez maintenant toutes les parties colorées qui restent. Ce qui est rouge, c'est le carré de l’hypoténuse, tout ce qui est vert, c'est le grand carré, les deux pièces bleues constituent le petit carré.
Maintenant, jouez au puzzle, reconstituez le carré bleu : deux pièces, tout le monde devrait y parvenir. Ensuite le carré vert, trois pièces, tu sauras faire Océane ?
La jolie jeune fille haussa les épaules avec une moue hautaine.
— Vous avez donc reconstitué les carrés des côtés. Voici le plus difficile, et c'est là le but de toutes ces manipulations, si vous réussissez à faire coïncider en les disposant correctement toutes les pièces vertes et bleues sur le carré rouge, vous aurez prouvé le théorème de Pythagore. Carré vert plus carré bleu égale carré rouge. Allez-y, solution dans cinq minutes. Levez la main dès que vous avez réussi...
— Bien Mathilde.
— Bien Valentin. Arrête de te retourner Océane.
— Bien Charles-Henri. Morgane, cherche par toi même, cesse de te lever sans cesse pour jeter des coups d’œil de mouche. Ça te fait rire Valentin ?
Bon, voici la solution, regardez au tableau !

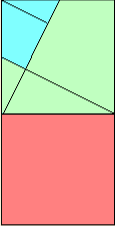
Vous pouvez voir que toutes les pièces du puzzle occupent exactement la surface du carré rouge, donc le carré du petit côté plus le carré du grand côté égale le carré de l’hypoténuse de notre triangle rectangle, CQFD. Quelqu'un a des questions ?
— Moi, m'sieur, intervint Tony, à quoi ça sert ?
— À faire des puzzles ! s'écria Morgane.
— Très drôle Morgane. Sinon, qui a une idée ?
— Ben à rien ! s'aventura Clément.
— À part l'avis circonstancié de Clément ?
Valentin et Mathilde levèrent la main en même temps.
— Mathilde ?
— Je ne sais pas si c'est à moi de le dire car cette proposition vient en fait de Valentin.
— Vas-y, dit Valentin en baissant le bras.
— Les bâtisseurs du moyen âge utilisaient un cas particulier de ce théorème pour tracer des angles droits.
— C'est exact Mathilde. Peux-tu développer l'idée ?
— Je préfère laisser Valentin.
— Alors, Valentin nous t'écoutons.
— Si je dessine un triangle avec des côtés de 3, 4 et 5 centimètres, j'obtiens obligatoirement un triangle rectangle.
— Peux-tu le démontrer ?
Les carrés des petits côtés de 3 et 4 centimètres font 9 et 16, leur somme fait 25 et 25 c'est le carré de 5, la dimension du plus grand côté, l’hypoténuse. Donc le triangle est obligatoirement rectangle. Les bâtisseurs se servaient d'équerres 3, 4, 5 pour tracer leurs angles droits pour que leurs murs soient évidemment d'équerre.
— Excellent Valentin. Quelqu'un pense-t-il à d'autres applications de ce théorème ? Personne ? Alors, imaginez une pièce rectangulaire, votre chambre par exemple. Vous désirez en connaître la surface...
— Pourquoi faire ? interrompit Clément.
— Décidément, tu es bien négatif aujourd'hui, Clément. Pour en connaître le prix par exemple ! Tu veux que je te donne le problème à faire ? Donc pour connaître la surface de votre chambre, il faut connaître sa longueur et sa largeur, ça vous le savez. Si vous pouvez mesurer la largeur « l », par exemple trois mètres mais pas sa longueur « L » à cause des meubles, vous mesurez la diagonale « D » de la pièce donc l’hypoténuse puisque les angles des murs de votre chambre sont des angles droits. Vous trouvez cinq mètres. La longueur pourra alors être calculée par la formule L² = D² – l². L² donc dans notre cas 5² moins 3², soit 25 moins 9, donc 16. La longueur de la chambre est donc la racine carrée de 16 donc 4 mètres car 16 = 4 fois 4.
— Là c'est facile parce que ça tombe juste, remarqua Amandine futée, mais si on avait obtenu par exemple 19 avec nos mesures, comment aurait-on fait ?
— C'est aussi facile, tu sors ta calculette de téléphone et tu cherches la racine carrée de 19, expliqua Gilles.
— Effectivement Gilles, c'est la solution moderne, la plus simple, la plus rapide, approuva le professeur.
— Et si on n'a pas de smartphone, hein ? objecta Tony prenant le relais de Clément.
— Avant les smartphones et les calculettes, il existait ce qu'on appelle une règle à calcul qui permettait de le faire. Il est également possible par une opération arithmétique de calculer soi-même, cela s'appelle extraire une racine carrée. Nous verrons cela dans une prochaine leçon. Les ordinateurs utilisent entre autres cette formule pour modéliser des pièces dans l'industrie.
— C'est bien ce que disait Clément, intervint Morgane, pour nous, ça ne sert à rien !
— Cette formule a eu un grand intérêt pour vous aujourd'hui, Morgane, elle a servi à quelque chose, elle vous a obligé à réfléchir donc à développer votre cerveau et certains d'entre-vous en ont grand besoin. C'est l'heure, rangez vos affaires et sortez dans le calme.
— Je préfère sortir dans le couloir, s'amusa Olivier qui s'était rapproché de Valentin. Alors, qu’est-ce qu’il t'a filé comme nouveau téléphone le prétentieux ?
— Je ne sais pas. Je regarderai ce soir chez moi, je ne veux pas lui donner la joie de me précipiter dessus, je suis sûr qu'il m'observe !
— Bien vu, il regarde vers nous. Je te signale que pour le puzzle, il a tout pompé sur toi.
— Je m'en doutais. Bah, ça lui a fait une petite compensation. Quel cours avons-nous maintenant ?
— Permanence, Radissel est absent et ensuite deux heures de gym avec Filedoux.